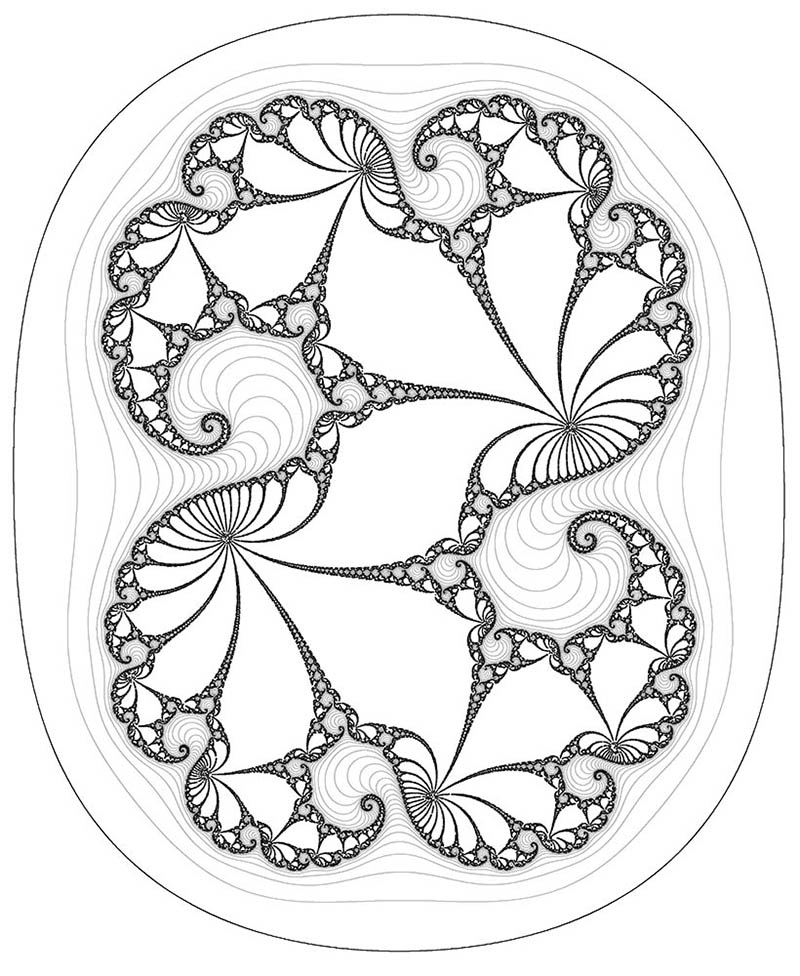
A Peek under the Hood

 

• Quilts

As the name suggests, the aim is to produce repeating seamless patterns like wallpapers. The quilts shown on this site are produced using one of the "chaotic orbit" formulas in the text.

The trick is to find values to plug into the formula which give visually interesting results. Here is one example:

 

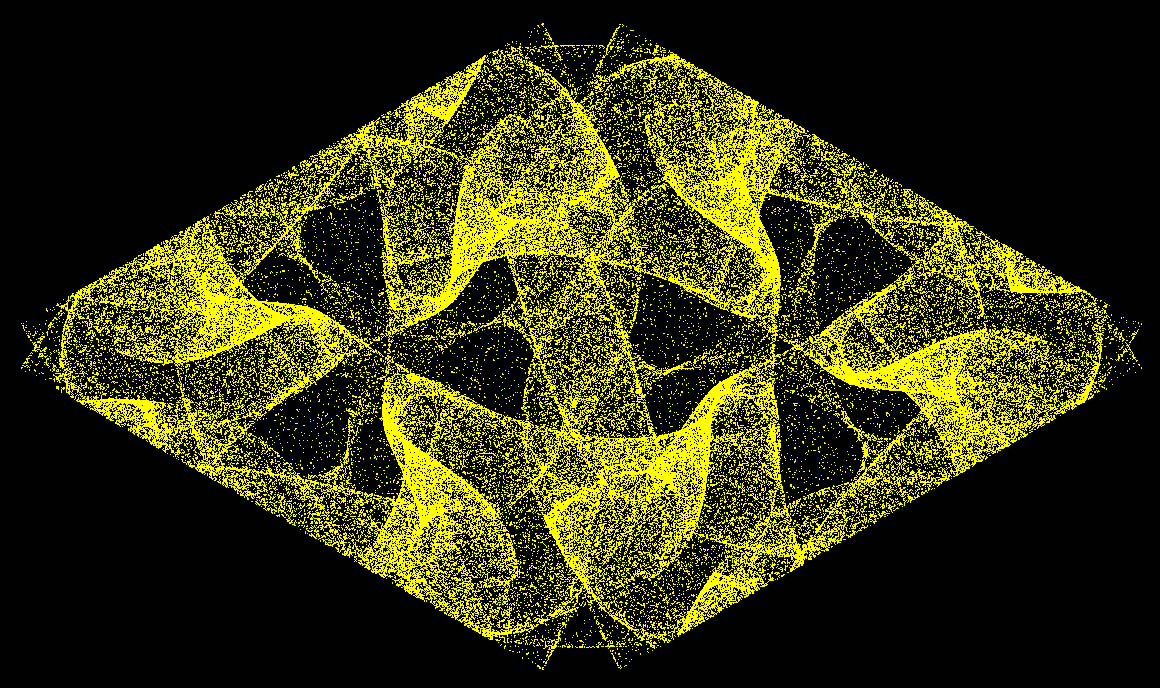
We borrow a 400 year-old method from Johannes Kepler ("Harmonices Mundi" 1619 - Diagram "G") and assemble 12 of the above like this:

 

Now to add some color. Using the rainbow as a model, we use Red to color the most crowded areas, Orange for slightly less dense areas ... down to the sparsest regions which we will color Violet.

 

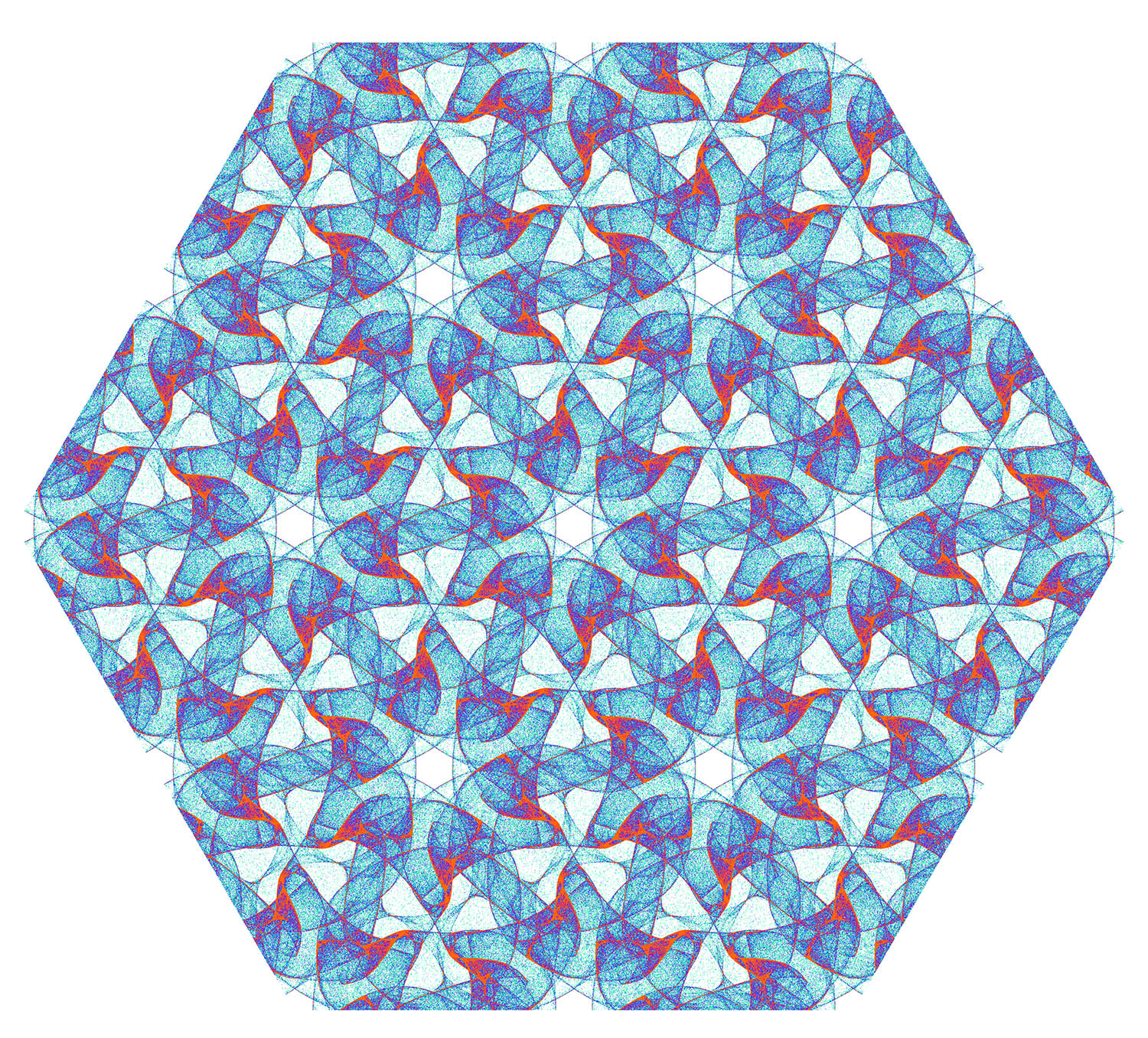
Combine hexagons and trim to get a wallpaper pattern.

 

We can add effects to the basic hexagonal shape:

 

 

__________________________________________________________________________

 

• Icons

There is no requirement for these to nest.

We start with this shape (based on the "Sunflower" image from the text):

 

With a bit of programming, we can transform the above to this:

Adding color as described above:

 

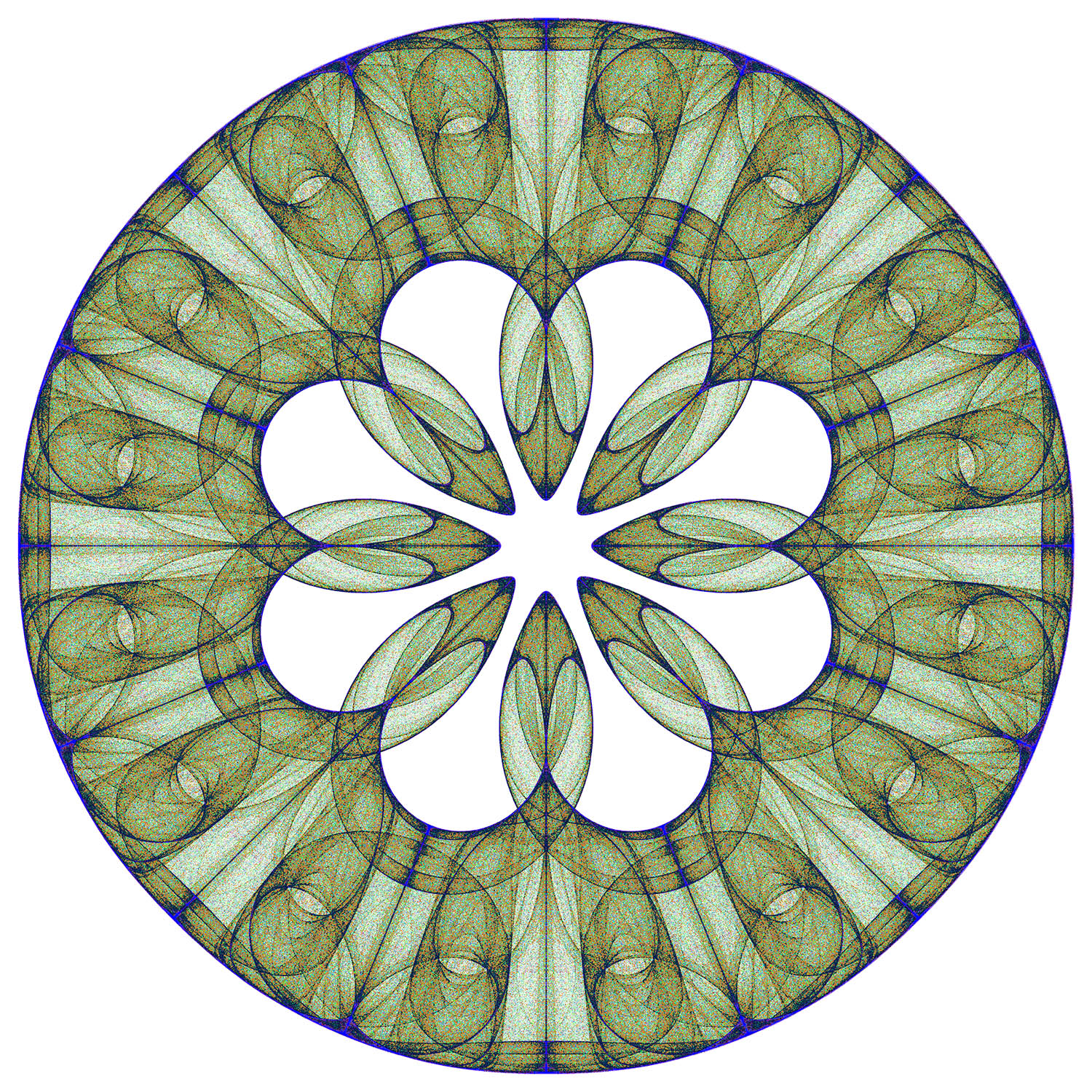
Or these:

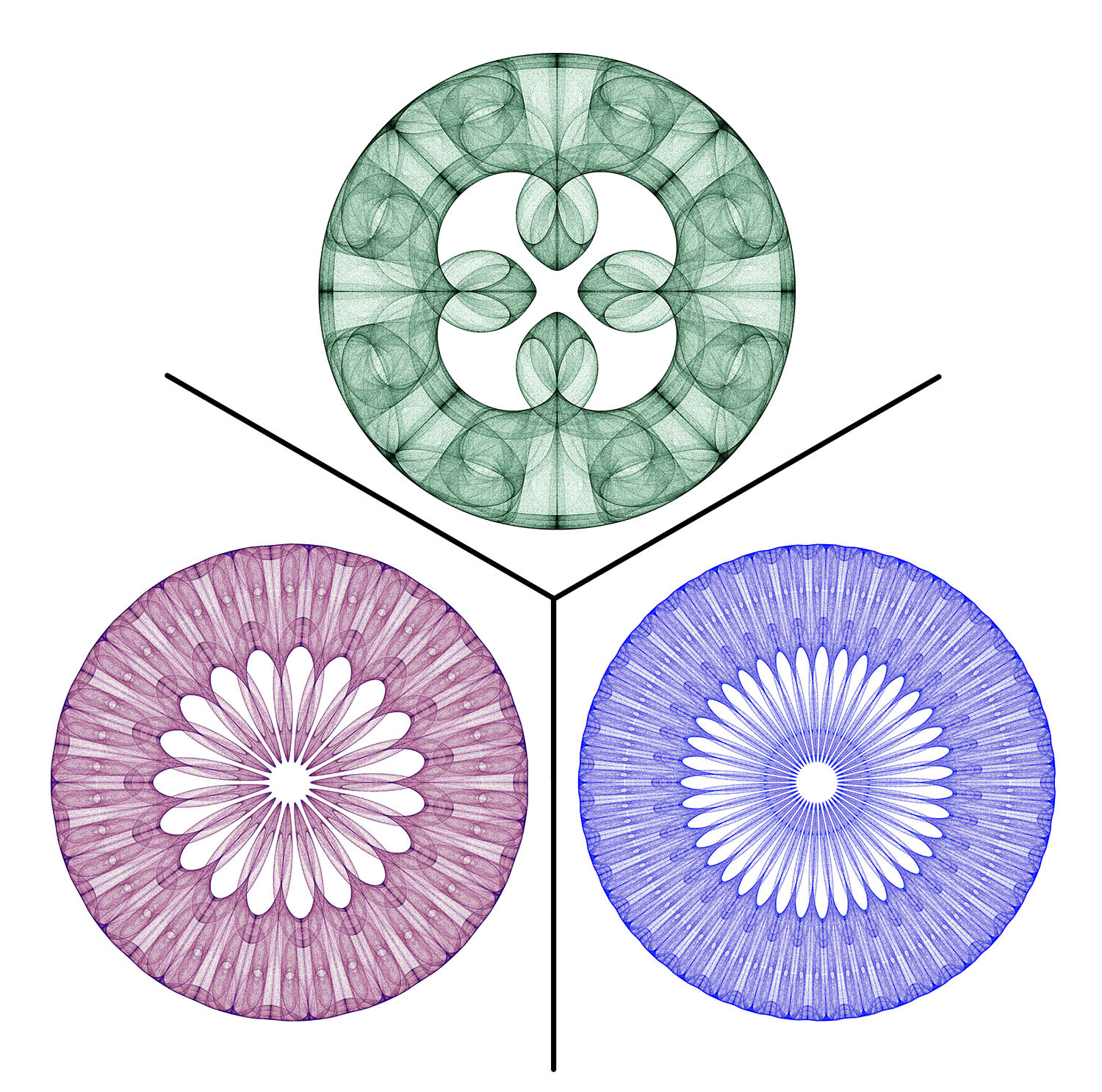
Note: Quilts and Icons are sometimes interchangeable. A suitable quilt element can sometimes be used as a standalone icon, and conversely, icons can sometimes be combined to form a quilt. There are several examples on this site.

______________________

 

• JULIA SETS

"..the Julia Set depends on the choice [of the key], but the surprise here is that it depends enourmously on it, so that by varying [it] you obtain an incredible variety of Julia Sets: some are a fatty cloud, others are a skinny bush of brambles, .. lots of them have sea-horse tails."

Adrien Douady - "The Beauty of Fractals"

The "key" value is shown under each of these examples: 

0.25

 

0

 

The underlying calulation is absurdly simple - expressed in words:

Think of a number (the "key")

Multiply it by itself

Add the "key"

Take what you got and repeat the previous two steps.

The resulting behavior can be translated into a color scheme.

 

 

-0.75

 

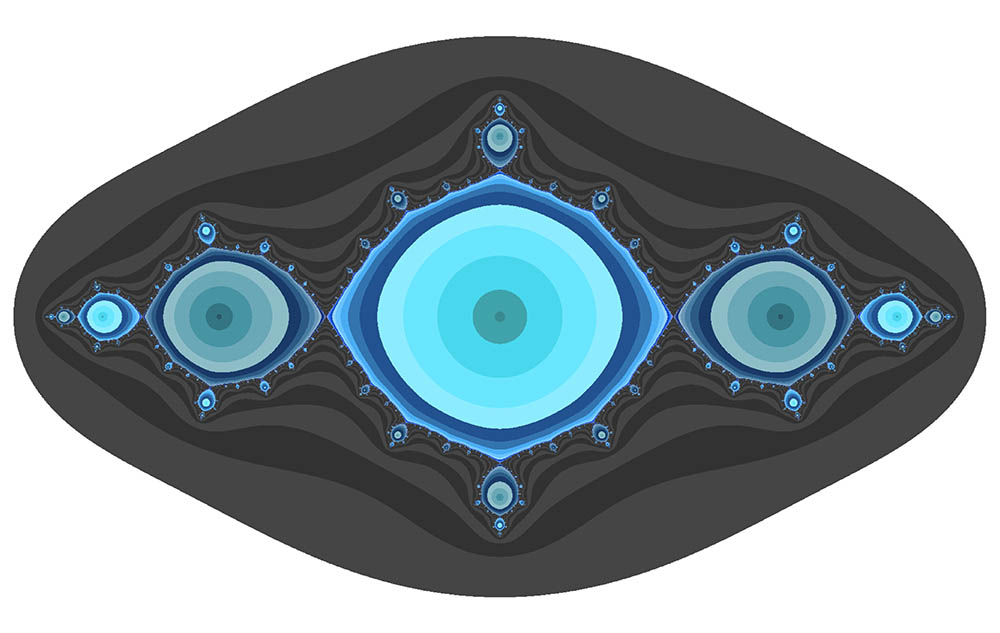
-1

 

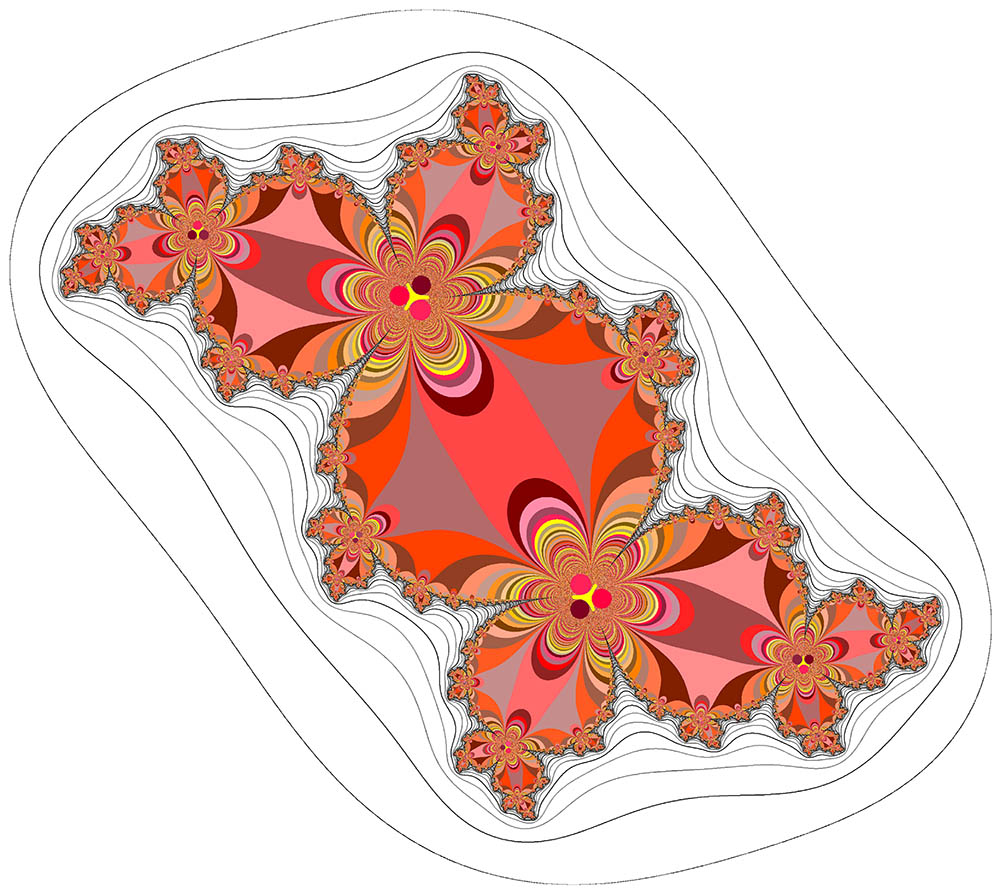
"Fat Rabbit" (-0.125,0.649519)

 

_____________________________

 

Variations on a Theme

 

______________________

 

• THE MANDELBROT SET

"It leaves us no way to become bored, because new things appear all the time, and no way to become lost, because familiar things come back time and time again. [..] Compared to actual fractals, its structures are more numerous, its harmonies are richer, and its unexpectedness is more unexpected."

Benoit Mandelbrot, from the video "Fractals: An Animated Discussion"

 

"This story hinges on a very plain formula .. Pick a constant c and let the original z be at the origin of the plane; replace z by z times z; add the constant c; repeat .. this shape is both overwhelmingly rich in detail and minutely subtle.."

"The Fractalist - Memoir of a Scientific Maverick" Benoit B. Mandelbrot

 

Each starting point "c" gives a different picture..

"Well-behaved" (after a shaky start):

 

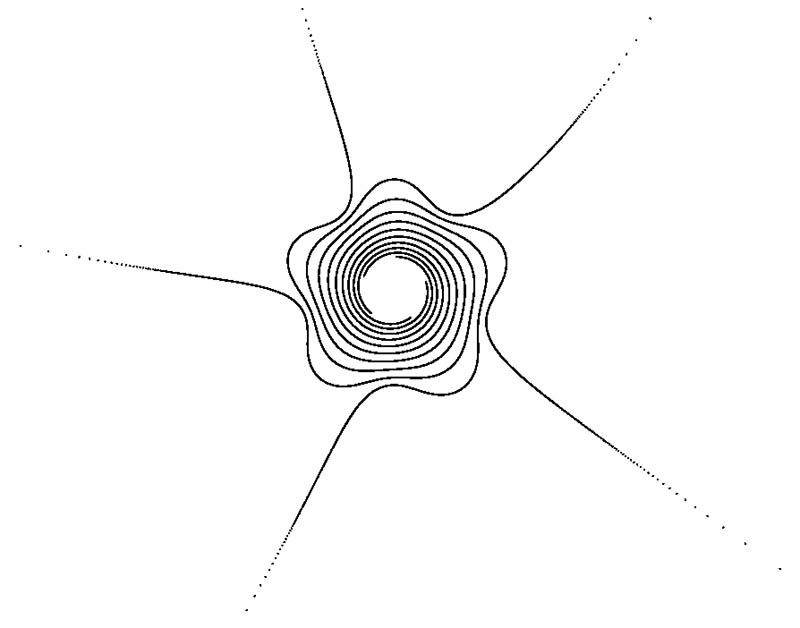
...and sometimes unsure of itself:

 

A single diagram demonstrates all possible behaviors:

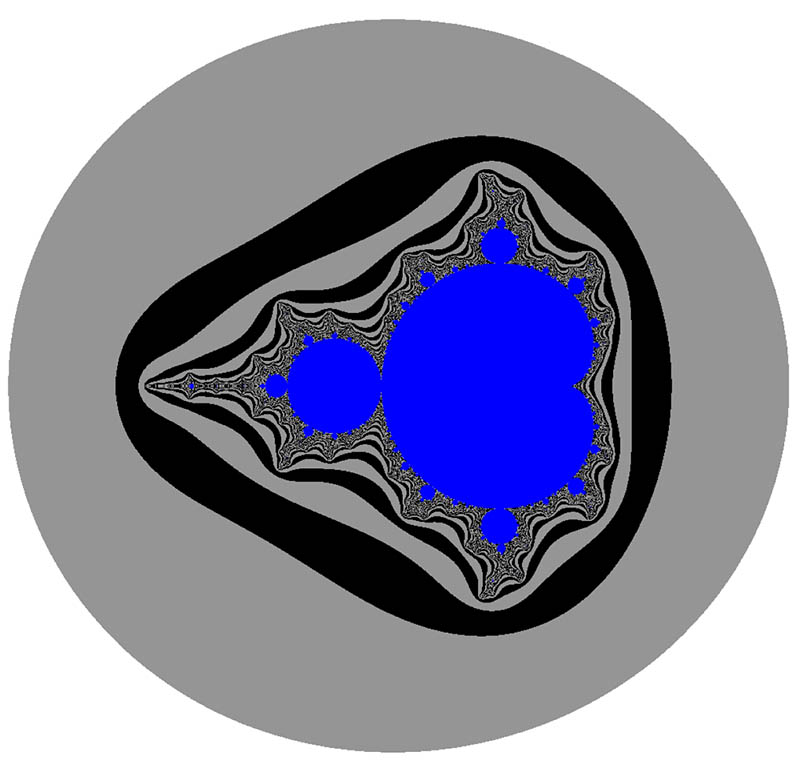
The "well-behaved" points are colored blue - this is the actual Mandelbrot Set, and the rest are in shades of gray. The "coastline" is where things get interesting from a technical and aesthetic point of view. The speed at which a point goes "bad" can be translated into a color scheme, and is the basis of many of the images on this website.

---

 

William Blake said he could see

Vistas of infinity

In the smallest speck of sand

Held in the hollow of his hand.

 

Models for this claim we've got

In the work of Mandelbrot:

Fractal diagrams partake

Of the essence sensed by Blake.

 

Basic forms will still prevail

Independent of the scale:

Viewed from far or viewed from near

Special signatures appear.

 

When you magnify a spot

What you had before, you've got.

Smaller, smaller, smaller yet,

Still the same details are set;

 

Finer than the finest hair

Blake's infinity is there,

Rich in structure all the way -

Just as the mystic poets say.

 

Prof. Jasper Memory

 

 

"You boil it in sawdust, you salt it in glue

You condense it with locusts and tape

Still keeping one principal object in view - 

To preserve its symmetrical shape."

Lewis Carroll - "The Hunting of the Snark"

--------------------

"Analysis does not owe its really significant successes of the last century to any mysterious use of the square root of minus one, but to the quite natural circumstance that one has infinitely more freedom of mathematical movement if he lets quantities vary in a plane instead of only on a line."

Leopold Kronecker